Gradient Descent

경사 하강법gradient descent은 다변수 함수의 극값을 찾는 가장 대표적인 알고리즘입니다. 이는 다음과 같은 반복적인 과정으로 이루어집니다.
  1. 적절한 초기값 $\bold{x}^{(0)}$을 선택합니다.
  2. 다음 과정을 $k=0, 1, 2, \cdots$ 에 대해 반복합니다.
    1. 현재 상태 $\bold{x}^{(k)}$로부터 경사 $\bold{d}^{(k)}$를 구합니다.
    2. 스텝 크기 $\alpha^{(k)}$를 결정합니다.
    3. $\bold{x}^{(k+1)} = \bold{x}^{(k)} + \alpha^{(k)} \bold{d}^{(k)}$와 같이 다음 상태를 구합니다.
    4. 정답에 충분히 가까워졌거나, 충분한 반복이 이루어졌다면 멈춥니다.

General Implement

다음과 같은 Booth 함수에 적용해봅시다. 
def Booth(x1, x2):
    return (x1 + 2 * x2 - 7) ** 2 + (2 * x1 + x2 - 5) ** 2
Booth 함수는 $(x_1=1, x_2=3)$에서 $0$을 최솟값으로 갖습니다. 한편 경사를 구하기 위해 함수의 도함수를 구해야 합니다. Booth 함수의 경우 식이 간단하므로 다음과 같이 $x_1$, $x_2$로부터 곧바로 미분값을 구할 수 있습니다. 
def Booth_diff(x1, x2):
    return 10 * x1 + 8 * x2 - 34, 8 * x1 + 10 * x2 - 38
이제 처음 스텝 크기 $0.5$, 매 반복마다 스텝 크기가 $0.9$배가 되도록 하여 경사 하강을 $100$번 반복해보겠습니다. 
# Initial state
x1 = x2 = 0

# Set step size and rate
step_size = 0.5
step_rate = 0.9

# Store history
his_1 = [x1]
his_2 = [x2]

for it in range(100):
    grad_x1, grad_x2 = Booth_diff(x1, x2)
    
    # Normalization
    grad_norm = (grad_x1 * grad_x1 + grad_x2 * grad_x2) ** .5
    
    # Descent to gradient
    x1 -= grad_x1 / grad_norm * step_size
    x2 -= grad_x2 / grad_norm * step_size
    
    # Store history
    his_1.append(x1)
    his_2.append(x2)
    
    # Adjust step size
    step_size *= step_rate

print(Booth(x1, x2), x1, x2)
# 3.239771779471502e-14 1.0000000424250683 3.000000042424757
$x_1$, $x_2$가 $1$, $3$으로부터 $10^{-7}$이내의 절대 오차를 가지며 이때의 함숫값은 $3.24\times 10^{-14}$로 $0$에 충분히 가까운 값임을 확인할 수 있습니다. 스텝 크기와 감소 비율, 반복 횟수를 적절히 변경하면 더 정확한 값을 얻을 수도 있습니다. 이때 정답에 충분히 가까워져 grad_norm이 $0$이 될 경우 반복을 중단해야 합니다. 위의 과정을 그림으로 나타내면 다음과 같습니다. 등고선 그래프contour plot는 Booth 함수를 나타냅니다. $(0, 0)$에서 시작하여 점점 $(1, 3)$에 가까워짐을 확인할 수 있습니다. 
import matplotlib.pyplot as plt
import numpy as np

x_min, x_max = -3, 6
y_min, y_max = -2, 6
x = np.linspace(x_min, x_max, 100)
y = np.linspace(y_min, y_max, 100)
X, Y = np.meshgrid(x, y)
Z = Booth(X, Y)

fig, ax = plt.subplots(dpi=300)
CS = ax.contour(X, Y, Z, 6)
ax.clabel(CS, inline=True)
color = plt.cm.jet(np.linspace(0, 1, len(his_1)))
ax.scatter(his_1, his_2, color=color, marker='+', linewidths=0.5)
ax.plot(his_1, his_2, color='black', linewidth=1.0)

ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')

plt.savefig('gd_Booth_1.png', bbox_inches='tight')

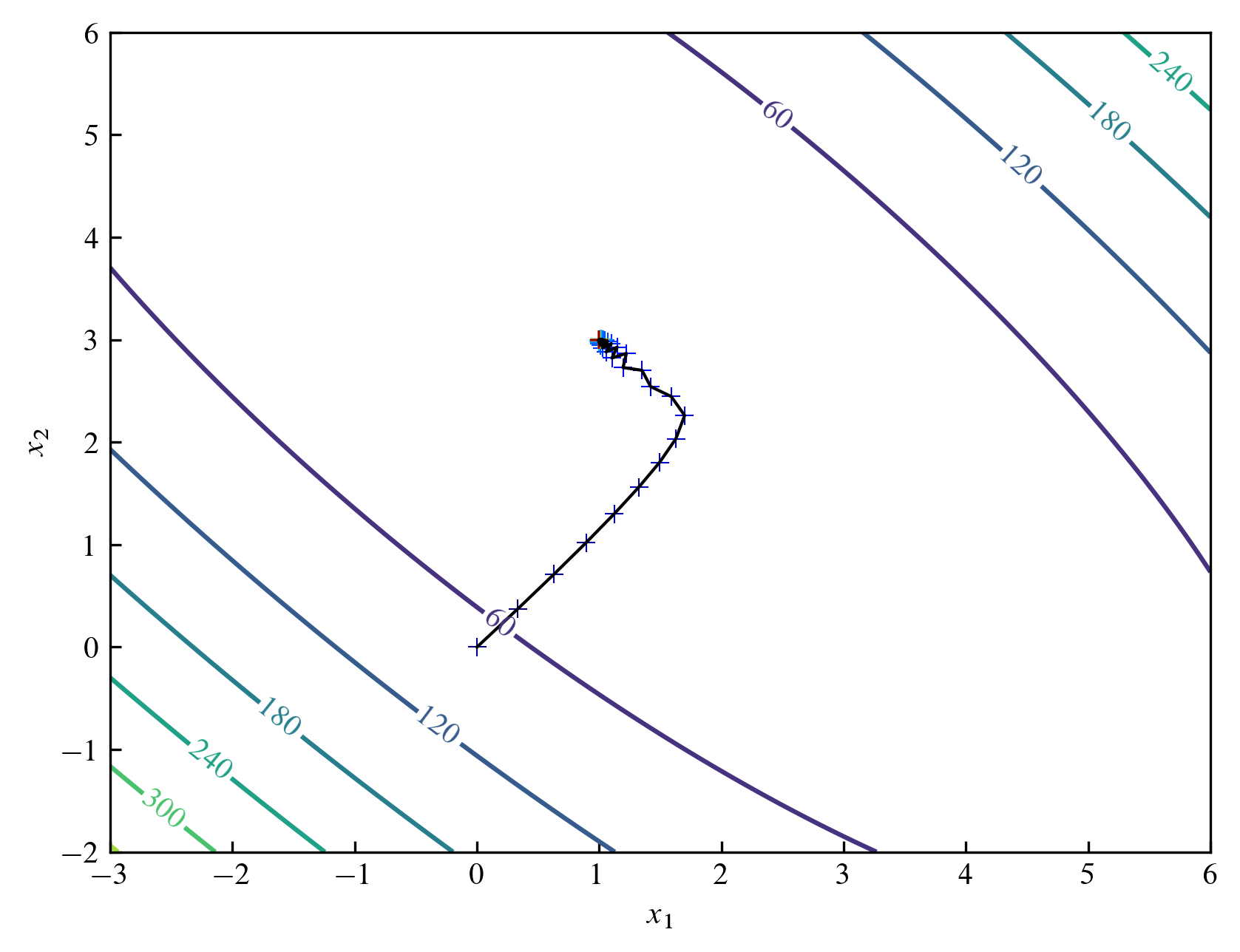
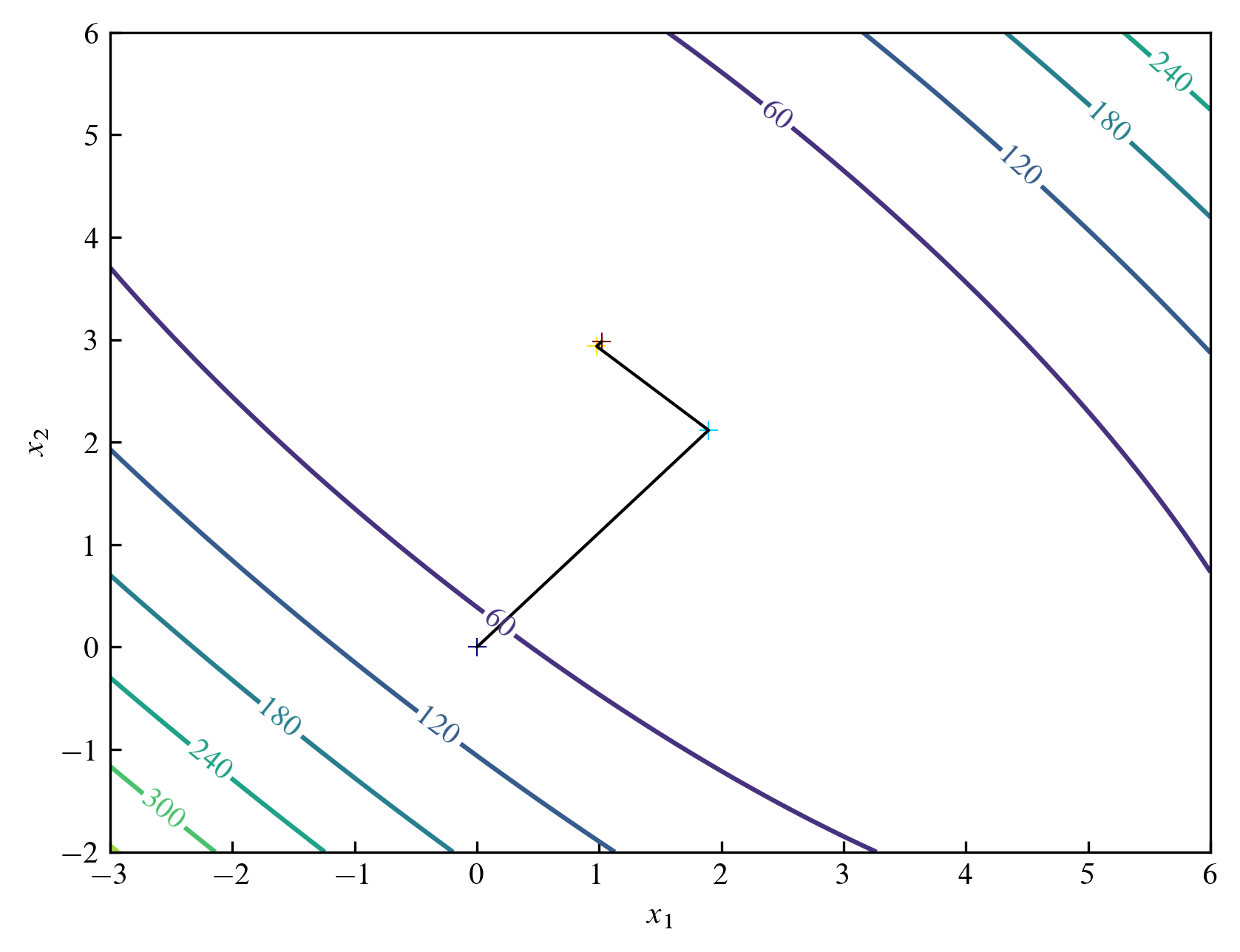
Zigzag pattern

스텝 크기 $\alpha^{(k)}$를 $f(\bold{x}^{(k)} + \alpha \bold{d}^{(k)})$가 최소가 되도록하는 $\alpha$로 선택하면 지그재그 패턴을 볼 수 있습니다. 그러한 $\alpha$를 선택하는 방법은 여러 가지일 수 있지만 여기서는 최소점을 포함하는 구간을 찾은 후 그 구간을 줄이는 방법을 선택하겠습니다. 
# Initial state
x1 = x2 = 0

# Store history
his_1 = [x1]
his_2 = [x2]

# Set enough unit step
unit_step = 1
for it in range(3):
    grad_x1, grad_x2 = Booth_diff(x1, x2)
    
    # Normalization
    grad_norm = (grad_x1 * grad_x1 + grad_x2 * grad_x2) ** .5
    grad_x1 /= grad_norm
    grad_x2 /= grad_norm
    
    # Func at t = 0
    now_func = Booth(x1, x2)
    
    # Find t such that func is bigger than now_func
    t = 1
    while 1:
        if now_func < Booth(x1 - grad_x1 * unit_step * t, x2 - grad_x2 * unit_step * t):
            t_f = t
            break
        t += 1
        
    # Reduce bracket length to (10/19)^20 = 2.7E-6
    left, right = 0, t_f
    for _ in range(20):
        _left = (10 * left + 9 * right) / 19
        _right = (9 * left + 10 * right) / 19
        if Booth(x1 - grad_x1 * unit_step * _left, x2 - grad_x2 * unit_step * _left) > Booth(x1 - grad_x1 * unit_step * _right, x2 - grad_x2 * unit_step * _right):
            left = _left
        else:
            right = _right
    
    # Descent to gradient
    x1 -= grad_x1 * unit_step * left
    x2 -= grad_x2 * unit_step * left
    
    his_1.append(x1)
    his_2.append(x2)

print(Booth(x1, x2), x1, x2)
# 0.0007198411684391871 1.0190842544172256 2.9811474775435425
다음 그림에서 볼 수 있듯이 각 상태를 연결하는 선이 지그재그 형태로 연결되며 세 번의 반복만으로도 빠르게 정답에 가까워짐을 확인할 수 있습니다.

Other functions

Rosenbrock function

$2$차원에서 Rosenbrock 함수는 다음과 같이 정의되며 계곡, 바나나 모양을 하고 있습니다. $$ f(x_1, x_2) = (1-x_1)^2 + 100(x_2 - x_1^2)^2 $$ 이 함수는 $(1, 1)$에서 $f(1, 1) = 0$의 최솟값을 가집니다. 도함수를 구하는 것은 어렵지 않지만 이번엔 중심차분을 이용하여 계산해보겠습니다. 여기서는 $h=10^{-6}$을 선택하였습니다. 더 정확한 미분값을 얻기 위해 더 작은 $h$를 선택하거나 충분히 작을 경우 복소 스텝 미분complex step differentiation을 고려할 수 있습니다. 
def Rosenbrock(x1, x2):
    return (1 - x1) ** 2 + 100 * (x2 - x1 ** 2) ** 2
def Rosenbrock_diff(x1, x2):
    h = 1e-6
    return ((Rosenbrock(x1 + h, x2) - Rosenbrock(x1 - h, x2)) / 2 / h,
            (Rosenbrock(x1, x2 + h) - Rosenbrock(x1, x2 - h)) / 2 / h)
이제 함수를 Rosenbrock으로 바꾸고 시작점을 $(-1.5, -0.5)$로 조금 변화시켜보겠습니다. 
def general_gradient_descent(func, func_diff, x1=0, x2=0, step_size=0.5, step_rate=0.99, iter=1000):
    # Store history
    his_1 = [x1]
    his_2 = [x2]
    
    for it in range(iter):
        grad_x1, grad_x2 = func_diff(x1, x2)
        
        # Normalization
        grad_norm = (grad_x1 * grad_x1 + grad_x2 * grad_x2) ** .5
        
        # Descent to gradient
        x1 -= grad_x1 / grad_norm * step_size
        x2 -= grad_x2 / grad_norm * step_size
        
        # Store history
        his_1.append(x1)
        his_2.append(x2)
        
        # Adjust step size
        step_size *= step_rate
    
    print(func(x1, x2), x1, x2)
    return his_1, his_2
his_1, his_2 = general_gradient_descent(Rosenbrock, Rosenbrock_diff, -1.5, -0.5)
# 0.291012879050753 0.46121627668208737 0.210027911326332
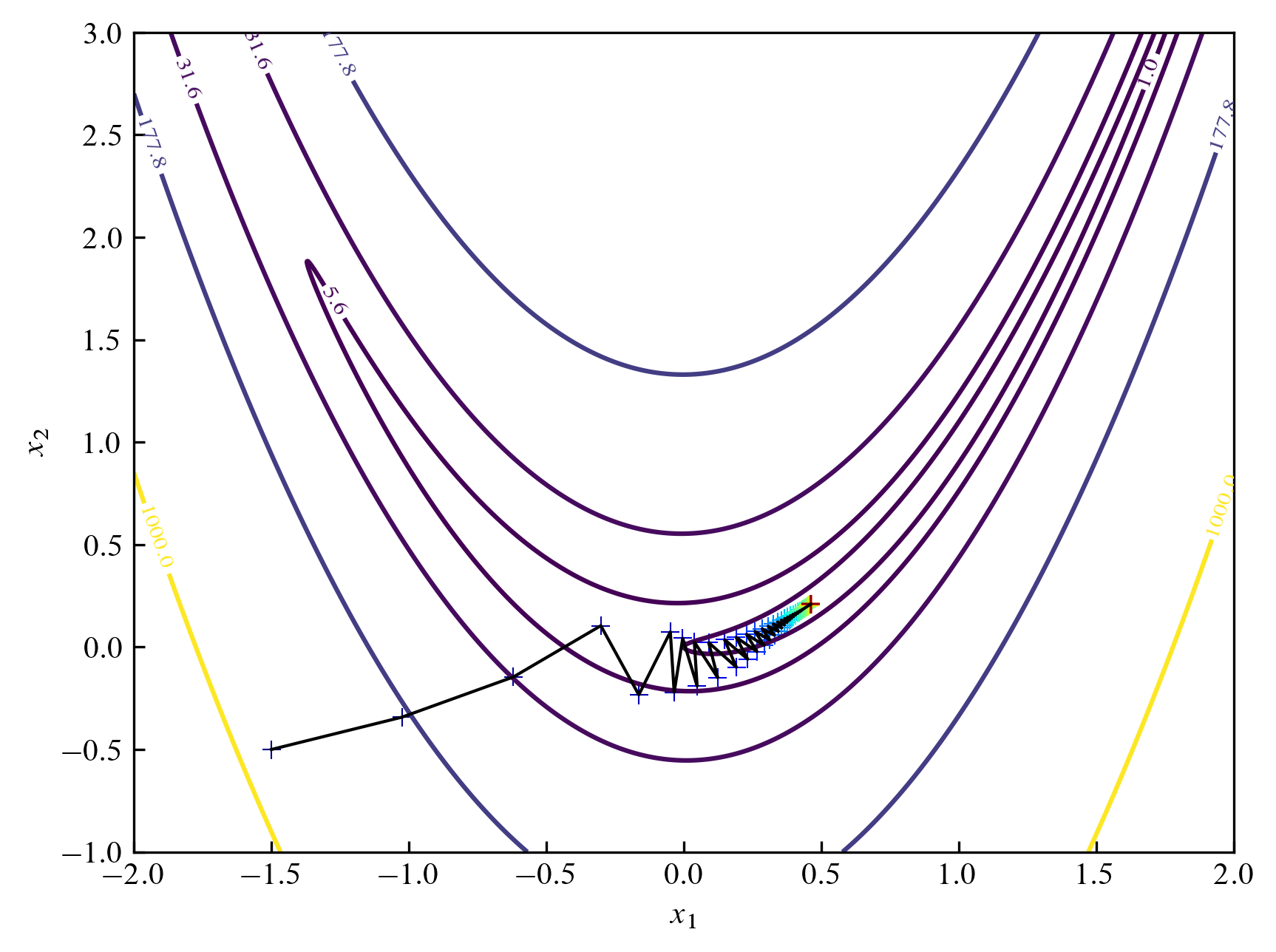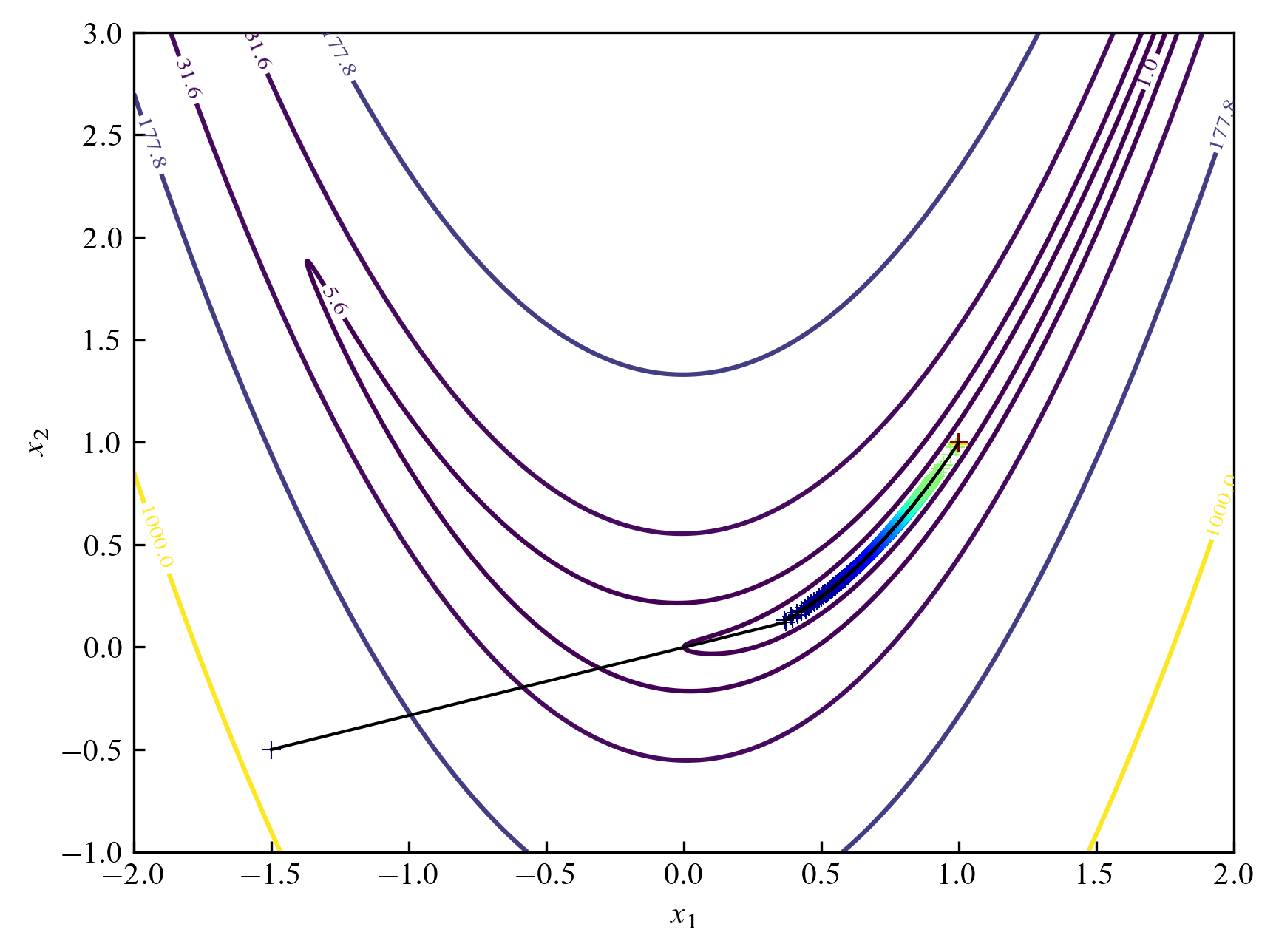
점점 $(1, 1)$에 가까워지고는 있지만 스텝 크기가 너무 작아져서 수렴하고 있는 모습을 보입니다. 스탭 변화율을 $0.99$로 하고 $1000$번 반복했을 때 다음과 같이 정답에 조금 더 접근하고 있습니다. 적절한 스탭과 반복 횟수를 선택하는 것이 중요하다는 것을 알 수 있습니다. 이번엔 지그재그 형태의 경사 하강법을 사용해봅시다. 반복 횟수가 $1000$회 정도일 때 $(0.9997, 0.9994)$ 정도로 가까워집니다. 
def general_gradient_descent_zigzag(func, func_diff, x1=0, x2=0, unit_step=1, iter=1000):
    # Store history
    his_1 = [x1]
    his_2 = [x2]
    
    for it in range(iter):
        grad_x1, grad_x2 = func_diff(x1, x2)
        
        # Normalization
        grad_norm = (grad_x1 * grad_x1 + grad_x2 * grad_x2) ** .5
        grad_x1 /= grad_norm
        grad_x2 /= grad_norm
        
        # Func at t = 0
        now_func = func(x1, x2)
        
        # Find t such that func is bigger than now_func
        t = 1
        while 1:
            if now_func < func(x1 - grad_x1 * unit_step * t, x2 - grad_x2 * unit_step * t):
                t_f = t
                break
            t += 1
            
        # Reduce bracket length to (10/19)^20 = 2.7E-6
        left, right = 0, t_f
        for _ in range(20):
            _left = (10 * left + 9 * right) / 19
            _right = (9 * left + 10 * right) / 19
            if func(x1 - grad_x1 * unit_step * _left, x2 - grad_x2 * unit_step * _left) > func(x1 - grad_x1 * unit_step * _right, x2 - grad_x2 * unit_step * _right):
                left = _left
            else:
                right = _right
        
        # Descent to gradient
        x1 -= grad_x1 * unit_step * left
        x2 -= grad_x2 * unit_step * left
        
        his_1.append(x1)
        his_2.append(x2)
    
    print(func(x1, x2), x1, x2)
    return his_1, his_2
his_1, his_2 = general_gradient_descent_zigzag(Rosenbrock, Rosenbrock_diff, -1.5, -0.5)

Himmelblau's function

Himmelblau 함수는 다음과 같이 정의되며 $4$개의 같은 함숫값 $0$을 가지는 극솟값이 존재합니다. $$ f(x_1, x_2) = (x_1^2 + x_2 - 11)^2 + (x_1 + x_2^2-7)^2 $$ 
def Himmelblau(x1, x2):
    return (x1 ** 2 + x2 - 11) ** 2 + (x1 + x2 ** 2 - 7) ** 2
def Himmelblau_diff(x1, x2):
    h = 1e-6
    return ((Himmelblau(x1 + h, x2) - Himmelblau(x1 - h, x2)) / 2 / h,
            (Himmelblau(x1, x2 + h) - Himmelblau(x1, x2 - h)) / 2 / h)
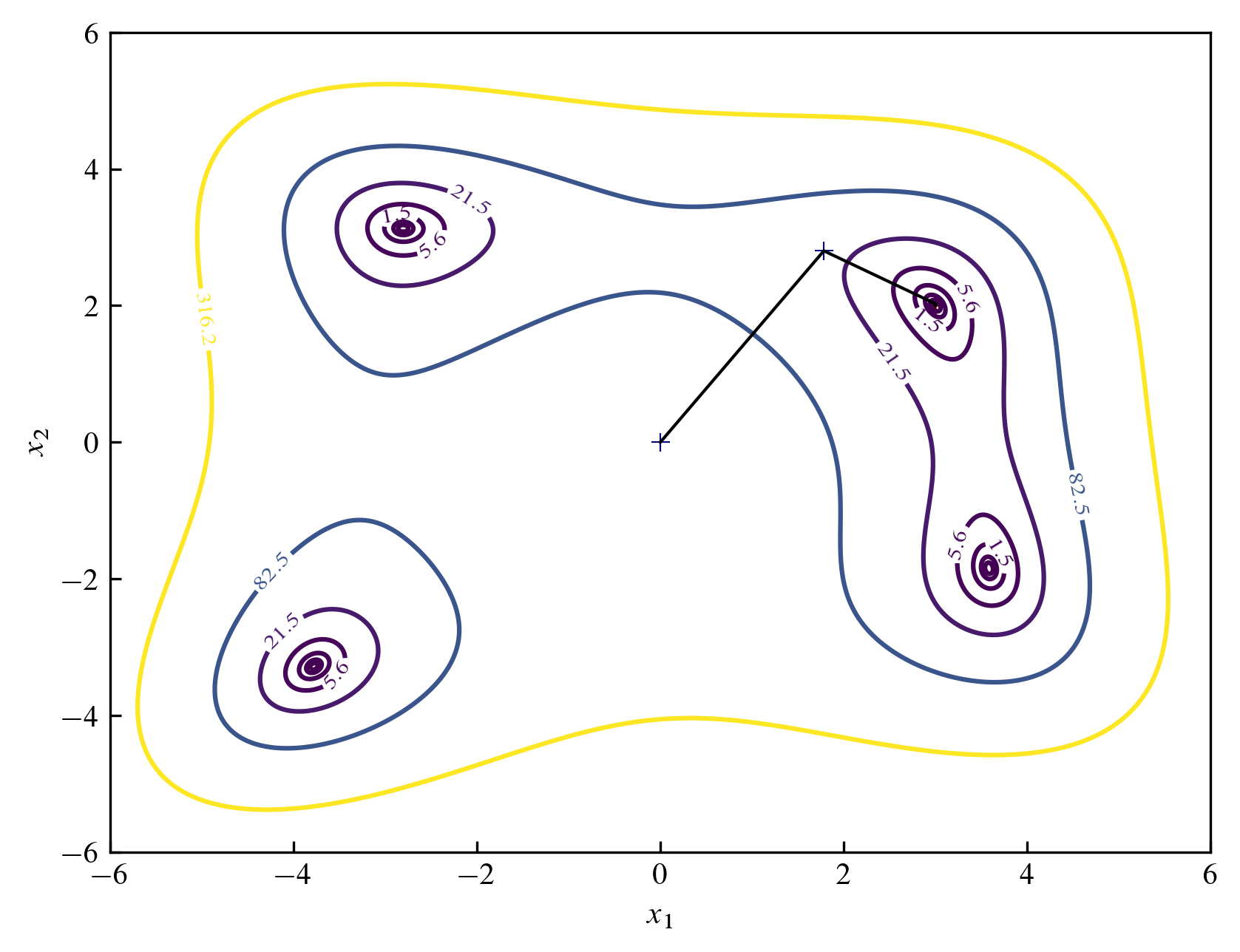
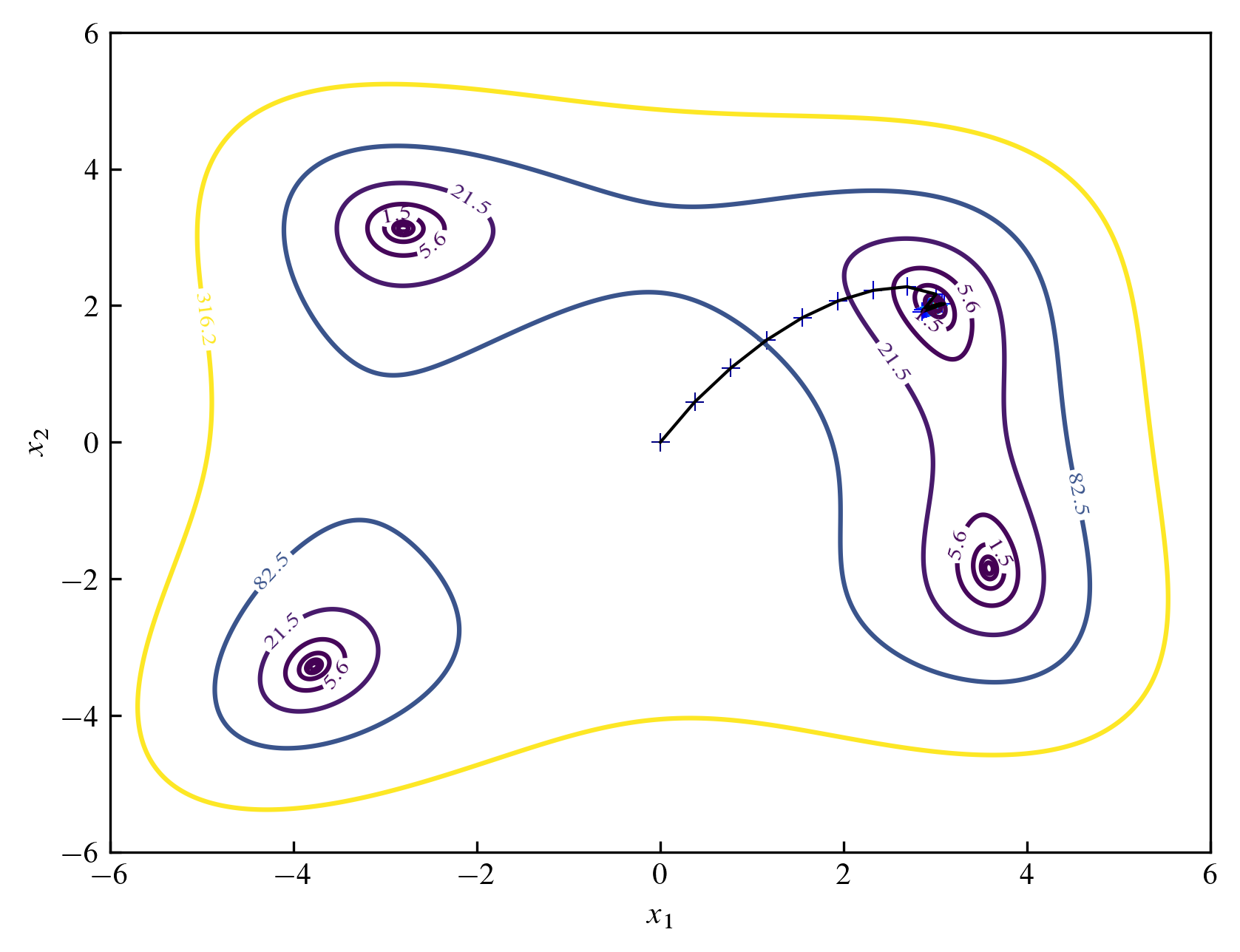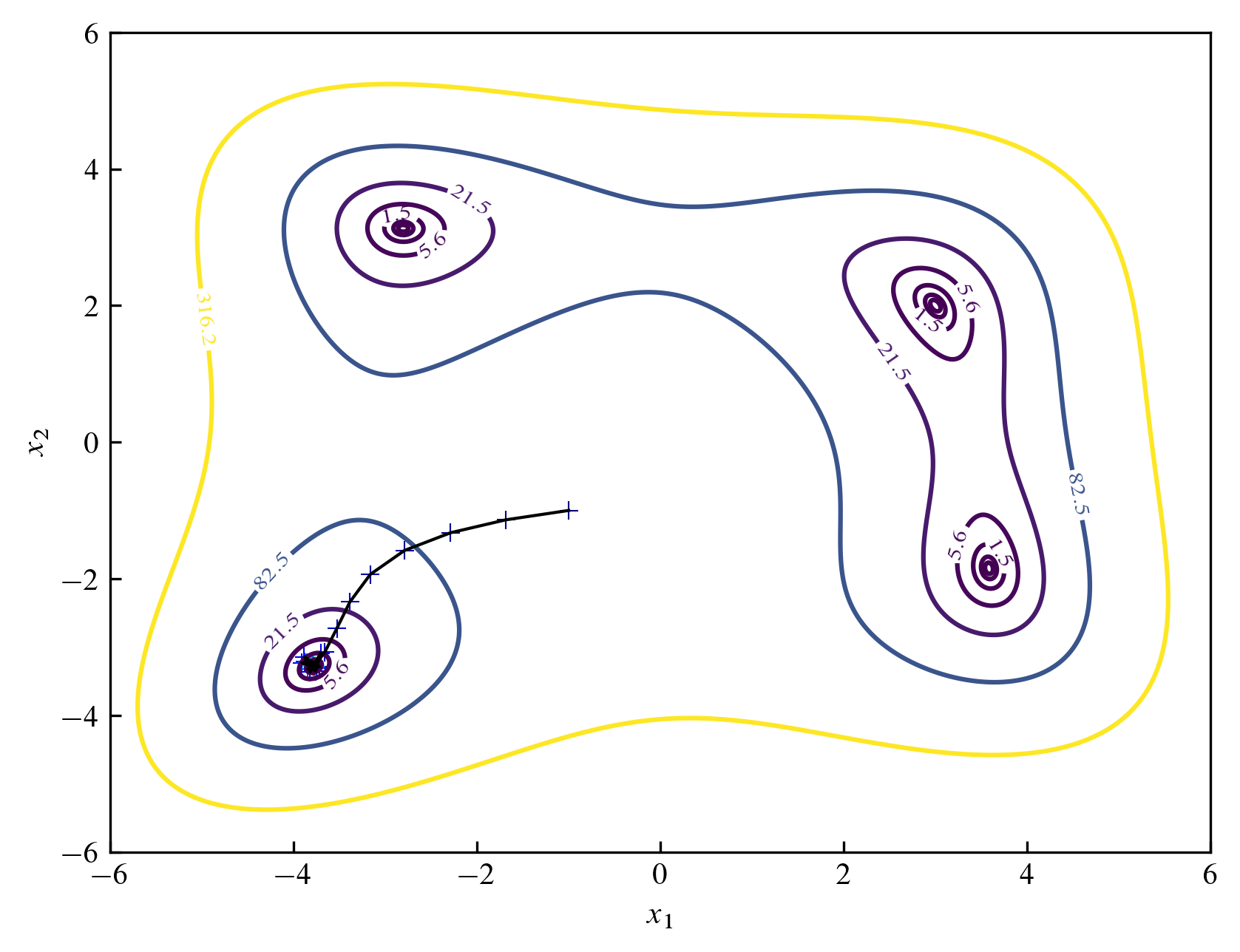
다음 그림은 $(0, 0)$에서 출발하여 스탭 크기 $0.7$, 스탭 변화율 $0.9$, 반복 횟수 $100$회일 때의 모습을 나타낸 것입니다. 다음 그림은 마찬가지로 $(0, 0)$에서 출발하여 지그재그 형태로 $100$회 반복한 후의 모습을 나타낸 것입니다. 함수의 극솟값은 다른 위치에도 있는데 이를 찾기 위해선 초기값을 적절히 변화시켜야 합니다. 다음은 초기값을 $(-1, -1)$으로 변화시켰을 때의 모습입니다.